Honlapom >> Infokar  >> 2. KRTR  >> 2.3.    2011.03
 

2.3. Az euklideszi tér projektív lezárása

Az euklideszi tér egy „inhomogenitása”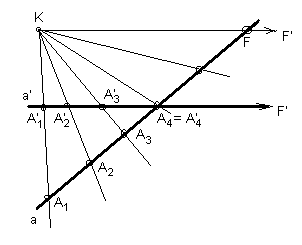egyenes pontjainak vetítése egyenesre

Ha az euklideszi síkban az a egyenes pontjait az X tengelyre vetítjük egy mindkettőn kívüli K pontból: az A, B, C, ... pontjain átmenő vetítősugarak az X tengelyen kimetszik az A’, B’, C’, ... vetületi pontokat. Az a egyenes minden pontjának megfelel egy vetületi pont, kivéve azt az F pontot, amelyen átmenő vetítősugár párhuzamos az X tengellyel.

A vetületi pontok az egyes vetítősugarak közös pontjai az X tengellyel. A KF vetítősugárnak és az X tengelynek azonban nincs közös pontja, csak az állásuk közös: párhuzamosak egymással.

Hasonló a helyzet, ha az euklideszi térben egy a sík pontjait vetítjük egy X síkra egy rajtuk kívül lévő K pontból. A sík azon pontjainál, amelyeken áthaladó vetítősugár párhuzamos az X síkkal, nem kapunk vetületi pontot az X síkon. Az ilyen vetítősugaraknak az X síkkal nincs közös pontjuk, de közös az állásuk az X sík egyik vele párhuzamos egyenesével.

Megszüntethető ez a kivételes helyzet, ha párhuzamos egyenesek egyező állását is „pontnak” nevezzük. Természetesen, ennek az önkényes elnevezésnek csak akkor van értelme, ha az így kapott geometria „értelmesen” használható. Szerencsére ez a helyzet.

Ha egy hosszú, egyenes vasúti pályán leállunk a sínek közé, látni véljük a horizonton azt a pontot, ahol a két sín találkozni látszik. Az euklideszi geometria évezredek által ismert törvényszerűségei jelentős műszaki alkotásokat tettek lehetővé. Hasonló geometriai törvényszerűségeket keresünk az előbb említett "látni vélt" pontokra is. Teljes általánosságban megteszi ezt a projektív geometria, de mi itt annak csak egyes eredményeit vezetjük be egyszerűen használható módon.

Az ideális pontokkal kibővített euklideszi tér

Az E3 euklideszi teret, a tér pontjainak halmazát "kibővítjük" további pontokkal, és így definiáljuk a kibővített H3 teret, amelynek kétféle pontja van: "közönséges" pontjai egyértelműen megfelelnek E3 pontjainak, illetve meghatározott módon definiált többi pontját "ideális" (csak ideákban létező) pontoknak nevezzük:

  • a tér minden egyenesének közönséges pontjain kívül még egy pontot tulajdonítunk, amelyet az illető egyenes ideális pontjának nevezünk,
  • egymással párhuzamos egyenesek ideális pontja megegyezik, és ez az egyenesek közös állását jellemzi (ami egy közös irányvektorral is jellemezhető),
  • egy sík ideális pontjainak halmazát az illető sík ideális egyenesének nevezzük,
  • a tér ideális pontjainak halmazát a tér ideális síkjának nevezzük.
  • párhuzamos síkok ideális egyenese megegyezik,
  • minden sík ideális egyenese -- és ezekkel minden ideális pont -- a tér ideális síkjában van.
Megjegyezzük, hogy az eulkideszi térben az egyenesek párhuzamossága ekvivalencia-reláció, és az egymással párhuzamos egyenesek ekvivalencia-osztályt alkotnak erre vonatkozóan. Az ideális pontok tehát egy-egy ilyen osztálynak felelnek meg.

Az így kibővített teret az euklideszi tér projektív lezárásának nevezik; mi röviden kibővített térnek, vagy a homogén térnek fogjuk nevezni. (A "homogén tér" elnevezést én szeretem, de -- tudtommal -- nem általánosan elfogadott elnevezés.) Ebben a pont, egyenes, illetve sík szavak egyaránt jelenthetnek „közönséges” és ideális pontot, egyenest, illetve síkot. (Az ideális pontokat magyarul szokták „végtelen távoli pontoknak” is nevezni, de ennél talán jobb a "távolpont"; németül: Fernpunkt. Minden egyenesnek csak egy ilyen pontja van.)

A kibővített síkban két egyenesnek, a kibővített térben két síknak mindig van közös pontja – közönséges, vagy ideális. Ha eltekintünk a közönséges és ideális pontok ilyen megkülönböztetéstől, akkor a kibővített tér valójában egy projektív tér. (Fordítva: ha a projektív térben kitüntetünk egy síkot, és ezt ideális síknak nevezzük, akkor a tér többi részében az euklideszi geometria érvényes.) A számítógépi grafikában azonban mindig egy véges térrészt szemléltetünk, ezért az ideális pontoknak, illetve az őket tartalmazó ideális síknak kitüntetett szerepük van.

Homogén koordináták egy derékszögű koordináta-rendszerben

Az euklideszi tér pontjai a tér egy közönséges pontjához rögzített DKR-ben valós számhármasokkal adhatók meg. Az euklideszi tér valódi részhalmaza a kibővített térnek, az utóbbi pontjainak megadására három koordináta kevés.
 
A kibővített tér egy közönséges pontjához rögzített DKR-ben
  • egy  (x, y, z) koordinátájú közönséges pontnak megfeleltetjük az [x, y, z, 1] homogén koordinátákat, illetve az ezzel arányos számnégyesek mindegyikét (ezen arányos számnégyesek ekvivalencia-osztályát):
(x, y, z)  => [x, y, z, 1] ≈ h · [x, y, z, 1] = [h · x, h · y, h · z, h]; h ≠ 0.
  • A kibővített térben egy (x1, x2, x3) irányvektornak megfelelő ideális pontnak a [x1, x2, x3, 0] homogén koordinátákat feleltetjük meg, illetve az ezzel arányos számnégyesek mindegyikét (ezen arányos számnégyesek ekvivalencia-osztályát):
az (x1,x2,x3) állású egyenesek ideális pontja
      => [x1, x2, x3, 0] ≈ h · [x1, x2, x3, 0] = [h · x1, h · x2, h · x3, 0]; h ≠ 0.

Vegyük észre, hogy a [0,0,0,0] számnégyes ezek során nem szerepelt!

 Fordítva, ha [x1, x2, x3, x4] a kibővített tér egy pontjának homogén (-koordinátás) alakja, és
  • ha x4 ≠ 0, akkor ez „közönséges pont”, és Descartes-koordinátáit így kapjuk:
        [x1, x2, x3, x4] ≈ [x1/x4, x2/x4, x3/x4,1] => (x1/x4, x2/x4, x3/x4)
  •  ha x4 = 0, de x1, x2, x3 nem mind nulla, akkor  [x1, x2, x3, 0] ideális pont  (az euklideszi térben pontként nem létezik), és az erre illeszkedő egyenesek párhuzamosak az (x1, x2, x3) vektorral.
  • végül [0, 0, 0, 0] nem pont (algoritmusaink eredményeként nem állhat elő).
Az ideális pontokkal kibővített síkban egy pontnak három homogén koordinátája van, a harmadik szerepe ugyanaz, mint a térben a negyediké.

Egy pont homogén koordinátáit tartalmazó számnégyest a pont homogén-koordinátás alakjának, röviden, homogén alakjának nevezzük. A homogén alak koordinátait mi szögletes zárójelbe írjuk. A Descartes koordinátákat általában (x, y, z) -vel, a homogén koordinátákat [x1, x2, x3, x4] -gyel jelöljük, de néha használjuk majd az [x, y, z, h] jelölést is, ahol h = 0 vagy 1. A P pont Descartes-koordinátáit (px, py, pz)-vel, homogén koordinátáit [p1, p2, p3, p4] -gyel jelöljük. Két számnégyes arányosságát a ≈  vagy a ~ jellel jelöljük majd.

Minden pontnak több számnégyes is megfelel, amelyek az egymással arányos számnégyesek egy ekvivalencia osztályát alkotják.

Műveletekben egy pontot az egymással arányos négyesek közül bármelyik képviselheti. Az egymással arányos számnégyesek közül normált alakúnak (röviden normáltnak) nevezzük azt, amelyben x4 = 1, illetve ideális pontoknál azt, amelyben a többi koordináta négyzetösszege 1 (ekkor ezek a rá „illeszkedő” egyenesek irány-koszinuszai).

Az ideális pontok homogén alakjának koordinátai közül az utolsót, a nullát elhagyva, a többiek az illető ideális pontra illeszkedő (azon "átmenő") egyenesek egy irányvektorának koordinátai (a normált alakban egységvektor). Az ideális pontok normált alakja kétértelmű: [x1, x2, x3, 0] és [-x1, -x2, -x3, 0]; minden egyenesnek két, egymással ellentétes irányvektora van.

Néhány nevezetes pont homogén koordinátái

           Bármilyen c ≠ 0 számmal

  • [0, 0, 0, c]T az origó homogén alakja,

  • [c, 0, 0, 0]T, [0, c, 0, 0]T, [0, 0, c, 0]T az X, Y ill. Z tengely ideális pontja

  • az YZ (x = 0) koordináta-sík  pontjai: [0, y, z, h]T,

  • az XZ (y = 0) koordináta-sík; pontjai: [x, 0, z, h]T,

  • az XY (z = 0) koordináta-sík; pontjai: [x, y, 0, h]T.

„Homogén terünk” szerkezete (olvasmány)

Az euklideszi tér izomorf a valós számhármasok terével:

E3   ≅ R3 = { (x, y, z); x, y, z ∈ R }

Adott x, y, z, w ∈ R valós számok esetén a [x, y, z, w] számnégyessel arányos számnégyesek ekvivalencia-osztályt alkotnak (az "arányos" relációra vonatkozóan):

Ax,y,z,w  = { [ x·h, y·h, z·h, w·h ]; x, y, z, w, h ∈ R,  h ≠ 0}

Az E3  projektív lezárásával kapott homogén tér az ilyenek halmazával izomorf kivéve a [0, 0, 0, 0] egyetlen elem ekvivakencia-osztályát): 

H3 ≅ {Ax,y,z,w ; x, y, z,w ∈ R} \ { A0,0,0,0}

A homogén koordináták használata

A homogén-koordináták használata a számításokban föloldja a nem metsző párhuzamosok „kivételes” helyzetét, és a mátrix-szorzáson keresztül egységes formalizmust nyújt a geometriai transzformációk algoritmikus végrehajtásához

A következő fejezetekben látni fogjuk, hogy a grafikában használt affin és projektív transzformációkban pontok homogén alakját szorozzuk 4x4-es mátrixokkal, és az egymásutáni transzformációk mátrixuk szorzatával adhatók meg.

A gyakorlatban geometriai feladatainkat a szokásos módon Descartes- koordinátákkal fogalmazzuk meg, és az eredményeket ugyanígy várjuk. Ha a számítások során valamihez homogén koordinátákra van szükségünk, akkor
  • előbb áttérünk homogén koordinátákra: a pontok Descartes-koordinátáihoz hozzáírunk még egy, 1 értékű koordinátát,
  • ezekkel végrehajtjuk a kívánt műveleteket,  
  • majd az eredmények értékelése előtt a koordináták arányos átalakításával visszatérünk Descartes-koordinátákra (az utolsó, homogén koordinátával osztjuk a többit).
Ez utóbbi lépés előtt szükség lehet arra, hogy a tér egy véges befoglaló „dobozán” (a tengelyekkel párhuzamos állású téglalapján) kívüli elemeket elhagyjuk, „levágjuk”, amivel a műveletek során esetleg beférkőzött „ideális térelemeket” hagyjuk el (ezek az eredmény szempontjából többnyire amúgy sem szükségesek).

A kibővített sík egy egyszerű szemléltetése (olv)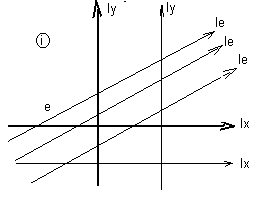a homogén sík ábrázolása

A szemléletes ábrázolás mindig megszokott konvenciók kérdése. Megállapodhatunk például abban, hogy a kibővített sík közönséges részét ugyanúgy ábrázoljuk, ahogy megszoktuk. Az ideális pontokat egyenesük végére tett nyílheggyel jelöljük, a sík ideális egyenesét pedig – nem tudván sehova „méretarányosan” elhelyezni – egy bekarikázott i betűvel jelöljük valahol az ábrán, jelezve, hogy "ő is van". A koordináta-tengelyek végére rejzolt nyílhegy képviselheti a tengely ideális pontját is; bár ennek eredeti jelentése: a koordináták növekedésébnek irányát jelzi.

Kis képzelőerővel egy ilyen ábra tekinthető a kibővített tér metszetének is a z = 0 síkkal.

A projektív sík modellje minden olyan konstrukció, amelyben a sík különböző elemeinek és az ezek közötti viszonyoknak (relációknak) kölcsönösen egyértelmű megfelelőt definiálunk. Ilyenek: a projektív sík 3D euklideszi geometriai modellje, félgömb- és gömb modellje, nyílt körlemez modellje, stb. Ezekkel kapcsolatban az irodalomra utalunk.

A kibővített tér néhány tulajdonsága (olv)

  • A projektív síkon a pont és az egyenes, a projektív térben a pont és a sík duális fogalmak. (L. Projektv geometria.)
  • A projektív síkban (térben) négy (öt), hármasával nem kollineáris pont kijelöl egy projektív koordináta-rendszert, amelyre vonatkozóan a sík (tér) pontjai egyértelműen jellemezhetők három (négy) projektív koordinátájukkal.
  • A projektív térben egy pontra illeszkedő egyeneseket sugársornak, egy egyenesre illeszkedő pontokat pontsornak, egy egyenesre illeszkedő síkokat síksornak nevezzük. A kibővített tér egy ideális pontjára illeszkedő sugársor elemei, illetve egy ideális egyenesre illeszkedő síkjai a tér közönséges (euklideszi) részében egymással párhuzamosak.
  • Az euklideszi térben az egyenest egy pontja (a síkot egy egyenese, a teret egy síkja) két részre osztja.
  • A kibővített térben az egyenest egy pontja nem osztja két félre; az egyenes ideális pontján keresztül mindkét irányban „körbejárható”. Az egyenes pontjaira jellemző „ciklikus sorrendjük”.
  • Az egyenest két pontja ketté osztja, amelyek közül az egyik tartalmazza sz ideális pontot.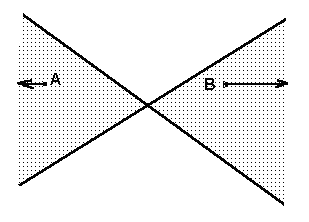A-projekiv-sik-ket-resze Hasonlóan a síkot két egyenese, a teret két síkja ketté osztja. A síkban egy közönséges ponton átmenő két egyenes két darab "kettős kúpra" osztja a síkot (az ábrán az A és B pontok egyenesük ideális pontján keresztül összeköthetők).  Ugyanígy két részre osztja a síkot  egy ideális ponton átmenő két egyenes (az euklideszi részben párhuzamosak). Egy egyenes "két oldala csak úgy értelmezhető, mint az egyenes és a sík ideális egyenese áltak "közrezárt" két félsík!

Az egyenes és sík egyenletének homogén alakja

  • A kibővített síkban egy egyenese megadható egy valós számhármassal:
    e = [e1, e2, e3], és az egyenes tetszőleges X = [x1, x2, x3]T pontjára:

e · X = [e1,  e2, e3] · [x1, x2, x3]T= e1·x1 + e2·x2 + e3·x3 = 0

  • Az [e1, e2, e3] számhármast az egyenes „vonalkoordinátáinak” nevezzük. Ezeket éppúgy meg lehet szorozni egy nullától különböző számmal, mint a pontok homogén koordinátáit.

  • A fenti egyenletű e = [e1,  e2, e3] egyenes ideális pontja: Ie = [ e2, _ e1, 0].

  • Ez az egyenlet az egyenesek korábban bemutatott "homogén implicit egyenletének" általánosítása úgy, hogy az egyenes ideális pontjára is teljesüljön.  (Ha közönséges pontok esetén a nullától különböző x3 együtthatóval osztjuk az egyenlet mindkét oldalát, az egyenes „közönséges” homogén egyenletét kapjuk.)

  • Annak az egyenesnek, amely a sík minden [x1, x2, 0]T ideális pontjára illeszkedik, a vonalkoordinátái nyilván [0,0,1]. Ez a sík ideális egyenesének homogén alakja.

  • Az e egyenesen kívüli X pontokra az e ·X skalárszorzat nem nulla. Az egyenes "egyik oldalán"  az (e ·X) · sign(x3) előjele pozitív, a másikban negatív. (A sign(x3) tényező azért kell, mert X és –X ugyanaz a pont! Az "egyenes egyik oldala" kifejezésre még visszatérünk.)

A sík egyenletének homogén-koordinátás alakja

  • A kibővített tér egy síkja megadható egy valós számnégyessel: s = [s1, s2, s3, s4], és a sík valamennyi X = [x1, x2, x3, x4]T pontjára:

s · X = [s1, s2, s3, s4] · [x1, x2, x3, x4]T= s1·x1 + s2·x2 + s3·x3 + s4·x4 = 0

Az [s1, s2, s3, s4] számnégyest a sík „síkkoordinátáinak” nevezhetjük. A síkkoordinátákat éppúgy meg lehet szorozni egy nullától különböző számmal, mint a pontok homogén koordinátáit. (Közönséges pontok esetén a nullától különböző x4 összetevővel osztva a sík „közönséges” homogén egyenletét kapjuk.)

  • Az s síkon kívüli X pontokra az s·X skalárszorzat nem nulla. A sík egyik oldalán (t.i. a sík és a tér ideális síkja által közrezárt egyik féltérben) az (s·X)·sign(x4) előjele pozitív, a másikban negatív. (X és –X ugyanaz a pont!)

  • Az egyenes  és a sík paraméteres egyenlete a kibővített térben az ideális pontokra nem használható.
A lap tetejérea lap tetejére