Honlapom >> Infokar  >>  Grafika-Jegyzet  >> 2. KRTR  >> 2.1. KR   2011.03
 

2.1. Koordináta-rendszereink az euklideszi térben

 

A ti-vel jelölt részek tartalmát "tudni illik". Ezeket az olvasó már biztos tanulta valahol, így ez itt csak ismétlés. Ezek ismerete a vizsgán nem érdem, nem-ismerete hátrány lehet.  
Az  olv[asmány]  jelű részek olyan olvasmányok, amelyek  nem-ismerete nem jelent hátrányt.
Ha egyik jelzés sem szerepel, azt persze egyszerűen: tudni kell.
A „koordináta-rendszer” szót KR-nek fogjuk rövidíteni, de tessék rendesen kiolvasni!

2.1.1. A Descartes-féle derékszögű koordináta-rendszer   (ti)
2.1.2. A pontok és a vektorok típusának definíciójáról  (olv)
2.1.3. A síkbeli polárkoordináták 
2.1.4. Gömbkoordináták, térbeli polár-koordináták
2.1.5. Baricentrikus koordináták
2.1.6. Alakzat megadása pontjainak koordinátáival   (olv)

2.1.1. A Descartes-féle derékszögű KR (ti)

Két különböző pont meghatároz egy egyenest, három nem kollineáris (nem egy egyenesbe eső) pont egy síkot, négy nem kom-planáris (nem egy síkba eső) pont meghatározza (kifeszíti) a teret. Egy további "egységpont" segítségével metrikát lehet bevezetni.

A tér (sík) egy DKR-ét kijelöli öt (négy) "független"  pont. (Független: amelyek közül egyik három) sem esik egy egyenesbe.)

A térben egy derékszögű koordináta-rendszert kijelöl egy kezdőpont (origó, O), és egy ortonormált bázis: három egymásra páronként merőleges egységvektor: i, j és k. (A síkban: két egységvektor.) (A szövegben a DKR rövidítést fogjuk használni, de olvasás közbe célszerű mindig kiolvasni: derékszögű koordináta-rendszer.)

A kezdőpontból a tér (a sík) egy pontjába vezető irányított szakaszt (vektort) az illető pont helyvektorának nevezzük. Egy pont koordinátái: a helyvektor tengelyekre eső merőleges vetületének előjeles hossza.  Az  r = (x, y, z) helyvektorú pont  koordinátái:

              x = |r| · cos x;  y = |r| · cos η;  z =  |r| · cos z;

Szavakkal: a pont helyvektorának hossza, szorozva a helyvektor és az X, az Y, illetve a Z tengely pozitív iránya által bezárt szög koszinuszával. Egységnyi (hely-)vektor koordinátái egyenlők a vektor és a tengelyek pozitív irányával bezárt szög koszinuszával. Egy egységvektor koordinátáit ezért nevezik a vektor iránykoszinuszainak is.
Descartes emlékére Descartes-félének nevezzük az ilyen koordináta-rendszert, bár -- olvasmányaim szerint -- Descartes maga  ferdeszögűt (is) használt.  Jegyzetünkben mi általában derékszögű DKR-t használunk. Az angol nyelvű irodalom Cartesian coordinates-ről beszél. (Descartes humanista szokásként használta a latinos Cartesius nevet..)
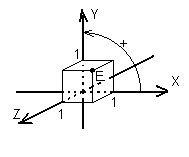
DKR-3D
Egy DKR többféleképpen is kijelölhető a térben. (Rendszeres matematikai megalapozás esetén egyet ezek közül definíciónak választanánk, és a többiről bizonyítanánk, hogy ezzel egyenértékűek.)

Meghatározza  egy kezdőpont (origó),  rajta átmenő három, páronként egymásra merőleges egyenes (a három tengely) és a tengelyeken kijelölt egy-egy egységpont (amelyek egyúttal meghatározzák a tengelyek irányítását is).

Meghatározható 5 "független" ponttal is: egy kezdőpont (az origó, O), az ezen átmenő három tengely egy-egy pontja, és egy a tengelyeken kívül eső egységpont (E). A tengelypontok meghatározzák a három tengely állását (eldöntetlenül hagyva ezek irányítását, és a rajtuk mért egységet), végül a térbeli egységpont meghatározza a tengelyeken mért távolság-egységet, eldöntve egyúttal a tengely irányítását is. Akkor nevezek "függetlennek" 5 pontot, ha közülük egyik három sem esik egy egyenesbe (és ekkor bármelyik négy kifeszíti a teret, illetve egyik négy sem esik egy síkba).

 Az egyes tengelyeken az egységnyi távolság eltérő hosszúságú is lehet; különösen ha az egyes tengelyeken különböző fizikai mennyiségeket mérünk föl. Például a hőmérséklet területi eloszlásának ábrázolásánál, a hőmérséklet-tengelyen nyilván más egység érvényes, mint a másik kettőn.

A tengelyeknek kiválaszthatjuk egy sorrendjét. Ebben a sorrendben a tengelyeket legtöbbször X, Y, Z-tengelynek nevezzük. A pontok koordinátáit eszerinti sorrendben számhármasként (számpárként), algebrai vektorként írjuk le.

A pontok koordinátáit jegyzetünkben egy oszlopvektor koordinátáinak tekintjük, de helykímélés céljából legtöbbször sorba kiterítve írjuk le. Ha ez félreértést okozhat (és nem felejtjük el), kitesszük a  transzponálás jelét is: (x, y, z)T.

Két tengely által kifeszített síkot koordináta-síknak nevezünk, és gyakran fogunk hivatkozni a z = 0 koordinátájú pontok XY-síkjára, és hasonlóan, az YZ-, illetve az XZ-síkra.

A térbeli DKR Z tengelyének irányítása az X és Y tengelyekhez képest kétféle lehet: az XY síknak egyik-, illetve másik oldala felé irányulhat. Eszerint a térbeli DKR kétféle irányításáról beszélünk: jobbsodrású (jobbos, jobbkezes), illetve balsodrású (balos, balkezes) KR-ről.

Jobbosnak nevezhetjük a KR-t, ha annak egy (i, j, k) ortogonális bázisával az (i × j) · k vegyes szorzat pozitív, ellenkező esetben balosnak. Szemléletesen: jobbsodrású KR-nek nevezzük, ha az X,Y,Z tengelyek jobb kezünk hüvelyk, mutató, és középső újjával fedésbe hozhatók. Ellenkező esetben balsodrásúnak. 
KKR3D
A sík egy DKR-je elhelyezhető egy térbeli DKR z = 0 síkjában. Ez jobbos, ha a Z tengely pozitív irányából nézve az X tengelyt az Y-ba az óra járásával ellentétes (CCLW, counter clock wise) forgás viszi át.

A képernyő koordináta-rendszerének (KKR) kezdőpontja a bal-felső sarokban van, X tengelye (szemből nézve) jobbra, Y tengelye lefelé irányul; ez így sikbeli balos rendszer. Térbeli tárgyak ábrázolásánál ezt a két tengelyt kiegészítjük egy hátrafelé irányuló Z tengellyel; ez így térbeli jobbos rendszer.
KKR3D-alk
A kép jelentését értelmezve kényelmesebb lehet a KR XY tengelyét jobbra és fölfelé irányítva, a Z tengelyt pedig hátrafelé elképzelni. Ez így balos térbeli rendszer.

Gyakran előfordul, hogy a világ tárgyxainak leírásánál az X- és Y síkot vesszük föl egy vízszintes síkban, és ekkor a Z tengely függőleges.

Mindenképpen tudatosítsuk egy-egy alkalmazásnál a tengelyek állását, mert különben -- különösen transzformációk után -- meglepő eredményekr juthatunk.

2.1.2. Pontok és vektorok típus-definíciójáról (olv.)

A térbeli DKR-ben a pontok és a vektorok egyaránt számhármasokkal (a síkban szám párokkal) adhatók meg: és programozásnál ezt a két típust legtöbbször nem különböztetik meg. Ezzel az elterjedt szokással nehéz szembeszegülni, de egyszer mégis érdemes belegondolni a kétfajta "objektum" különbözőségébe. Ha így definiáljuk a két típust:

    type Gxyz    = Real;    // vagy lehetne Double
    type Point3  = record x,y,z : Gxyz; end;
    type Vector3 = record x,y,z : Gxyz; end;

A Vector3 típus szabadvektort jelent: nincs helye, csak állása és hossza. A típus algebrai műveletei: összeadás, kivonás, szorzás számmal, skalár-szorzás és kereszt-szorzat. Definiálhatjuk még egy vektor abszolút értékét (hosszát), és - logikai függvényként - két vektor egyenlőségét.

A Point3 típussal, szigorúan véve, nincs értelme algebrai műveleteket végezni (lásd még alább), de két pont (algebrai alakjának) egyenlősége - egyezése -  logikai függvénnyel vizsgálható.

A két típus együtt is használható műveletekben típuskényszer (cast) alkalmazásával:.

Point3  P, Q,  R, S, P1;
Vector3 v, vp, d, dPQ;

vp  := Vector3(P);            // a P pont helyvektora
P   := Point3(v);             // a v helyvektor végpontja
dPQ := Vector3(Q)-Vector3(P); // a PQ vektor
P1  := Point3(Vector3(P)+d);  // P1: P eltolva a d vektorral
                                      // végül a PQR háromszög súlypontja:
S := Point3((Vector3(P)+Vector3(Q)+Vector3(R))/3.0

A kétféle típus szétválasztása a programban „szigorú típus-ellenőrzést” tenne lehetővé, de a típuskényszer gyakori használata kényelmetlen lenne a programozó számára. Ezért legtöbbször nem különböztetjük meg ezt a két típust; a pontokat is vektor típussal adják meg.

Emellett, egyes alkalmazások ugyancsak igényelhetik pontok algebrai műveleteit, például a mechanikában tömegpontok súlyozott összegét. (Bevezethető a tömegpont típus, amely tömeg típusú változóval szorozható és összegezhető.)

2.1.3. A síkbeli polárkoordináták

PKR

A sík egy polárkoordiáta-rendszerét meghatározza egy kezdőpont, egy ebből kiinduló félegyenes -- a polártengely -- és az ettől való pozitív elfordulás iránya. A polártengely általában egy DKR x-tengelye, a pozitív elfordulás iránya az x-tengely pozitív felét az y-tengely pozitív felébe viszi át.

Egy P pont polár-koordinátái: P = (r, ϕ); a pont r távolsága az O kezdőponttól (0 ≤ r), és ϕ polárszöge, az O-ból P-be vezető r sugár és a polártengely közötti szög (0 ≤ ϕ < 2π).

A polár-koordináták átszámítása derékszögű koordinátákba egyszerű. Fordítva, a polár-koordináták kiszámításánál a derékszögű koordinátából néhány triviális esetet kell megkülönböztetnünk.
 PK =>> DK
 DK =>> PK
x = r · cos ϕ,
y = r · sin ϕ		 r  = √ (x2+y2) és
ϕ = arctan(y/x),         ha sem x sem y nem 0,
   =   0,                      ha y = 0 és x > 0
   =   π,                      ha y = 0 és x < 0
   = +π/2,                   ha x = 0 és y > 0
   = -π/2,                    ha x = 0 és y < 0
   = meghatározatlan,  ha x = y = 0 (a pont a kezdőpont)

Polár-koordinátákat általában olyankor használunk, ha egy alkalmazás geometriai viszonyait így lehet kényelmesen és szemléletesen leírni. A legegyszerűbb példa erre a körmozgás. A PKR hátrányai: egy PKR-ből egy más kezdőpontú PKR-re (a koordináta- rendszer transzformációja) nehéz áttérni, a polárszög kiszámítása (az arctan függvény) költséges, a görbék érintőjének és normálisának kiszámítása nehéz.

2.1.4. Gömbkoordináták, térbeli polár-koordináták

GKR

Meghatározza az XY alapsík, a benne megadott polár-koordinátákkal és egy erre merőleges Z tengely.

Egy P = (r, ϕ, θ) pont gömbkoordinátái: a pont r távolsága O-tól (0 ≤ r), az r sugár alapsíkra eső vetületének polárszöge (0 ≤ ϕ < 2π), és a θ azimut, az r sugár és a Z tengely pozitív iránya közötti szög (0 ≤ θ ≤ π);

Gömbkoordinátákat használhatunk például tárgyak egy ponthoz viszonyított térbeli helyzetének és mozgásának leírásakor. Ugyancsak jól használhatók a földgömbön való, és az ahhoz képesti helyzet megadására; ilyenkor ϕ lényegében a földrajzi hosszúság, θ a földrajzi szélesség (de ezt ott az egyenlítő síkjától mérjük  (-π/2 ≤ θ ≤ +π/2).HKR

Az (r, ϕ, z = r · cos θ) értékeket a pont hengerkoordinátáinak nevezzük. 
 
A gömbkoordinátá átszámítása derékszögű koordinátákba - és vissza:
GKR =>> DKR DKR =>> GKR
Az r sugár vetülete az alapsíkra:

ρ = r · sin θ,  és ezzel:
     
x  = ρ · cos ϕ = r · sin θ · cos ϕ;
y  = ρ · sin ϕ =  r · sin θ · sin ϕ,
z  = r · cos θ		 r  = √(x2+y2+z2),
ρ = √(x2+y2)  (a z-től függetlenül)
ϕ =  mint a síkbeli PKR-nél,
θ =  arccos(z/r),    ha r nem 0,
   =  0,          ha ρ = (x = y = ) = 0 és z > 0
   =  π,          ha ρ = (x = y = ) = 0 és z < 0,
   =  meghatározatlan, ha r = x = y = z = 0

2.1.5. Baricentrikus koordináták

pontok tömegközéppontja

Ha  a sík P1, P2, P3 pontjai kifeszítik a síkot (nem kollineárisak, nem esnek egy egyenesbe) és helyvektoruk v1, v2, v3, akkor a sík bármely S pontjának s helyvektora előállítható ezek súlyozott átlagaként; azaz található hozzá olyan m1, m2, m3 számhármas, amellyel a S pont s helyvektora:


         m1·v1 +  m2·v2 + m3·v3                                                                          mi
  s = ------------------------------ =  b1·v1 +  b2·v2 + b3·v3;    bi  = --------------------
            m1 +  m2 +  m3                                                           m1 +  m2 + m3

Az  m1, m2, m3 számokat (illetve a b1, b2, b3  számokat) az S pont (-nak a P1, P2, P3  rendszerre vonatkozó) baricentrikus koordinátáinak nevezzük.  Szemléletesen: a P i, pontokba helyezett mi súlyok (tömegek) súlypontja (tömegközéppontja) S
Ezek homogén koordináták, vagyis tetszőleges, nullától különböző µ számmal µ·m1, µ·m2, µ·m3 is ugyanannak a pontnak a baricentrikus koordinátái; minden pontnak végtelen sok, egymással arányos baricentrikus koordináta-hármasa van. Ezek közül normáltnak tekintjük azt, amelyre:  m1 +  m2 + m3  = 1. (A fenti képletben  m1 +  m2 + m3 reciprokával szoroztuk az mi koordinátákat.) 

Ha mindhárom súly pozitív, a súlypont a háromszögön belül van; külső pontok esetén vannak negatív súlyok is, és ha valamelyik súly 0, akkor a súlypont a háromszögnek a megfelelő ponttal szemközti oldalán van.  (Negatív súlyok esetén a fizikai analógiát erőltetve talán gondolhatunk fölfelé húzó erőkre.)

A baricentrikus koordináták affin invariánsak: ha {m i} egy  P pontnak a {Pi} alappontokra vonatkozó baricentrikus koordinátái, akkor bármely A affin transzformációval a transzformált  A·P pontnak a {A·Pi} alappontokra vonatkozó baricentrikus koordinátái is ugyanezek.
Ha az En-ben (n≥1) az A0, A1, …, An  (n+1) pont kifeszíti a teret (nincsenek egy n-1 dimenziós altérben), akkor az {Ai} pontok a tér egy „vonatkoztatási rendszerét” alkotják. Ebben a, tér minden X pontjához található a λ0, λ1, …, λn valós számok rendszere (λi negatív is lehet) úgy, hogy
X = λ0A0 + λ1A1 +…+ λnAn ;        és   λ0 + λ1 +…+λn = 1 legyen; 
Ekkor a {λi} számokat az X pontnak az {Ai} pontokra vonatkozó baricentrikus koordinátáinak nevezzük.

Az E3-ban (a térben) négy, E2-ben (a síkban) három, az E1-ben (az egyenesen) két baricentrikus koordinátája van egy pontnak.

Fizikában X az {Ai} pontokban elhelyezett {λi} (nem negatív súlyok) súlypontja. N

Az {λi} homogén jellegű koordináták: tetszőleges h ≠ 0 valós számmal h·{λi} = {h·λi} is ugyanannak a pontnak a baricentrikus koordinátái. 

Affin transzformációk nem változtatják meg egy pont baricentrikus koordinátáit: egy pont affin transzformáltjának baricentrikus koordinátái a vonatkoztatási rendszer (alappontjainak) affin transzformáltjában ugyanazok, mint az eredeti pontéi az eredeti rendszerben.

Ha az alappontok egy konvex tartomány csúcsai, és egy pont ezekre vonatkozó baricentrikus koordinátái 0 és 1 közé esnek, akkor a pont az alappontok konvex burkán belül esnek.
Általánosan: E n-ben (az n dimenziós euklideszi térben) (n≥1)  n+1 alapponttal hasonlóan. Ha a súlyok mindegyike pozitív, akkor a súlypont az alappontok konvex burkán belülre esik.

A baricentrikus koordináták affin invariánsak: ha {mi} egy  P pontnak a {Pi} alappontokra vonatkozó baricentrikus koordinátái, akkor bármely A affin transzformációval az {mi} az  A·P pontnak a {A·Pi} alappontokra vonatkozó baricentrikus koordinátái is.

2.1.6 Alakzat megadása pontjainak koordinátáival (olv.)

A DKR a geometriai modellezés alapvető eszköze.

Egy geometriai alakzat egyenlete (vagy egyenlőtlensége, vagy egyenletrendszere): olyan egyenlőség (illetve egyenlőtlenség, vagy ilyenek rendszere) amely teljesül az alakzat minden pontjára és csak azokra a pontokra. Például a síkban 3x + 4y =8  egy egyenes egyenlete, 3x + 4y + 8 < 0 egy félsík egyenlőtlensége.

Az egyenes (általános) egyenlete: olyan paraméteres egyenlet, amely bármilyen adott paraméterekkel valamelyik egyenes egyenlete, és így minden egyenes egyenletét megkaphatjuk. Például: ax + by + c = 0 az egyenes (általános) egyenlete a síkban. (Az y = mx+b alak nem elég általános; mert az Y tengellyel párhuzamos egyenesek egyenlete nem ilyen. )

Egy alakzat egyenletének explicit alakja: y = f(x), illetve z = f(x, y). Például y = sqrt(r2-x2) egy félkör explicit egyenlete, amelyben az y koordináta ki van fejezve (explikálva) az x függvényében. Előnye y illetve z közvetlen kiszámíthatósága. Hátránya például az, hogy f csak egy értékű függvény lehet.

Egy egyenlet implicit alakja: g(x,y) = 0, illetve h(x,y,z) = 0; egyik koordináta sincs kifejezve (explikálva), de mindegyik kordináta benne értetődik (implikálva van). Például x2 +y2  = r2  egy teljes kör implicit egyenlete.

Egy alakzat paraméteres egyenlete (egyenlet rendszere) az alakzat pontjainak helyét fejezi ki valamilyen paraméterektől függően. A térben egy szakasz egyenlete így írható:
          r(t) = {x = a0 + t · a1,  y = b0 + t · b1,  z = c0 + t · c1; 0 ≤ t ≤ 1}, 
valamilyen x = a0, a1, b0, b1, c0, c1 együtthatókkal.

Egy gömb felszínének paraméteres egyenlete így (is) írható: 
     x  = ρ · sin θ · cos ϕ;  0 ≤ θ ≤ 2π; 0 ≤ ϕ ≤ π.
    y  = ρ · sin θ · sin ϕ,
    z  = ρ · cos θ;           

Térbeli felületek paraméteres megadása esetén a felület r = (x,y,z) pontjait az (u,v)  paraméterektől függő vektor-skalár függvénnyel adjuk meg:

              r = r( u,v ) = { x( u,v ), y( u,v ), z( u,v ) };  a ≤  u ≤  b, c ≤  v ≤  d

és a felület egy r 0 pontjához az u0, v0 értékek tartoznak, akkor ezeket az r0 pont Gauss-féle koordinátáinak nevezzük.  (Látható, hogy itt egy R2 => R3 függvényről van szó.) 

Egy geometriai alakzatot a számítógépben egyenletének (vagy  egyenlet- rendszerének, vagy egyenlőtlenségének) együtthatóival adhatunk meg, reprezentálunk, ezeket tároljuk, ezekkel az együtthatókkal számítva hajtjuk végre a különböző geometriai műveleteket.

A geometriai modellezés szempontjából egy alakzat egyenlete „jó”, ha belőle kiszámítható az alakzat érintőjének, normálisának egyenlete is, és ha alakja nem változik (invariáns) a KR transzformációja során. Az affin transzformációk nem változtatják meg a pontok baricentrikus koordinátáit.